VÍDEO DE CÁLCULO DE SOMBRAS SOBRE UN OBJETO
Calcular la sombra de un cuerpo se reduce a calcular la intersección de rectas y planos, las que representan a los rayos de luz y las superficies con las que se intersecan, respectivamente.

La sombra de un cono en sistema diédrico
Por el vértice A2 seguimos la dirección del rayo de luz hasta que intercepta el suelo en P. Proyectamos también en planta por A1 la dirección del rayo y en la intersección de la vertical por P con esta dirección obtenemos la sombra del vértice As en planta.
Desde As hacemos las tangentes e t a la circunferencia base del cono y obtenemos los puntos de tangencia M N desde los que hacemos segmentos hasta A1.
A1 M N es el sector circular de sombra propia en planta y en alzado subimos N M hasta la circunferencia y unimos con A2 teniendo así la sombra propia del alzado.
La sombra que arroja sobre la planta es la región As-M-A1-N menos el sector circular y sobre el alzado desde N2 hasta P.

La sombra arrojada y la línea que separa la luz de la sombra propia de un cuerpo son homólogas: cada punto del contorno que separa la luz de la sombra propia A y su sombra arrojada sobre el suelo A’, están alineados con el foco de luz O. El segmento que pasa por cada par de puntos de la silueta de sombra AB se cortan en la intersección (el eje) de su plano VAB con el plano de la sombra A’B’V’, en el mismo punto P donde se cortan sus homólogos A'B'

Hay dos tipos de sombra, la provocada por un punto de luz cercano que provoca que la sombra se irradie desde él y la que corresponde a una luz distante, semejante a la solar y cuyos rayos de luz se consideran paralelos.
En el primer caso siempre se proyecta la luz L sobre el suelo L’. L se alinea con el punto del que se quiere calcular la luz (p. ej. A) y L’ con la proyección en el suelo de ese punto (con A’). La intersección de LA y L’A’ es As, sombra del punto A desde L.
Cuando un segmento m del objeto es paralelo al suelo, su sombra ms es paralela a él.
Si no es paralelo (A A'), el segmento corta el suelo en un punto -A'- (o su prolongación), la sombra se proyecta entonces desde ese punto A', ya que la sombra de ese punto es él mismo.
VÍDEO SOBRE CÁLCULO DE SOMBRAS DEL CONO

En la luz distante se opera igual, con la salvedad de que los rayos de luz se consideran paralelos y por tanto sus proyecciones también. Tenemos dos direcciones: la dirección del rayo a por un punto P del objeto y su proyección sobre el suelo, la línea a’ que pasa por P’ (P'es la proyección ortogonal de P sobre el suelo).
Las líneas a a' provocan en su intersección el punto Ps, sombra de P.

Cuanto más cerca está el punto de luz del objeto, más se abre la sombra y se incrementa el área de esta.

Los diferentes valores en los tonos que hay sobre el objeto (oscuridad distinta en las partes del cuerpo)se deben a la reflexión de la luz, entre otros efectos:
http://calculo-de-reflejos.blogspot.com/
Luz que puede parecer distante por permanecer las líneas del contorno de la sombra paralelas, puede ser no obstante puntual debido a un efecto de convergencia de las paralelas propio de la perspectiva.

Si desde L’ hacemos la tangente a la base L’T’, tenemos que a partir de ese punto se separa la luz de la sombra. Como la figura es vertical, por T’ hacemos la vertical y localizamos en la intersección con la circunferencia el punto T que es el que corresponde al punto de tangencia de la sombra del círculo y de la generatriz TT’.
A la línea TT’ que separa la luz de la sombra se le llama línea separatriz.

Una figura puede definir su forma por medio de las sombras. A un único alzado corresponden múltiples posibilidades de combinación de volúmenes en planta.
Dos rectángulos en alzado se pueden interpretar, por ejemplo:

1-Como un prisma sólido saliente.

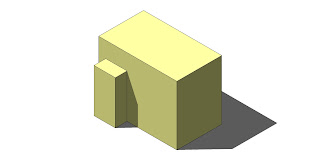
2-Como un prisma hueco, entre otros.


Para calcular la sombra que una figura proyecta sobre el plano vertical PV, se proyecta ortogonalmente sobre el plano horizontal PH, el punto del que se quiere calcular su sombra, por ejemplo V1 como proyección del vértice V. Por V (vértice del cono) trazamos la dirección del rayo de luz V en el espacio. Por V1 trazamos sobre el PH la recta d, que es la proyección ortogonal del rayo de luz que pasa por V. La intersección de rayo de luz y su proyección es Vs, punto de sombra de V si no hubiera un plano vertical delante.
Si por la intersección de d con el PV levantamos una recta vertical hasta que corte al rayo de luz obtenemos V’s que es la sombra de V sobre el plano vertical.
Desde las tangentes trazadas desde Vs al cono tenemos la sombra del contorno del mismo, si donde cortan esas tangentes al plano vertical lo unimos con V’s tenemos la sombra arrojada del cono sobre el PV.

Calcular la sombra sobre el plano vertical es en síntesis determinar la intersección del rayo de luz con el plano vertical, para ello pasamos un plano vertical por el rayo hasta que corte al PV. También se puede reducir a determinar las trazas del rayo de luz b, que son Vs (horizontal) Vs2 (vertical).

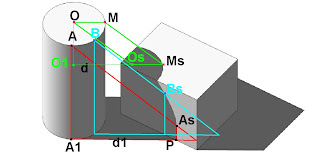
Para calcular la sombra del cilindro con luz distante (rayos paralelos que simulan luz solar) se proyecta la cara superior del cilindro: la sombra del centro A es As (intersección de rayo de luz y su proyección ortogonal sobre el suelo) ya que la dimensión de la circunferencia proyectada es igual a la del objeto por ser la cara superior del cilindro paralela al suelo.
Desde la sombra de la circunferencia de centro As se hacen las tangentes t p a la base del cilindro y en los puntos de tangencia se levantan verticales, que son las líneas que separan la luz de la sombra.

Tenemos la dirección del rayo de luz en planta y alzado (d1 d2), la traza horizontal As de esta recta es la sombra en planta del punto A, centro de la cara superior.
Desde la circunferencia de centro As se hacen las tangentes t p a la circunferencia en planta de centro A1. El punto Z1 de la tangente t al cilindro, se proyecta en el alzado para diferenciar en el mismo la separación de luz y sombra, análogamente se hace en el punto diametralmente opuesto de la tangente a p.

Sombra propia y arrojada de un cilindro con un cono apoyado en su cara superior.
Tenemos la dirección de los rayos de luz definida por r, la intersección de estar recta con su proyección sobre el suelo r' (recta que pasa por V1, esto es, la proyección ortogonal de V sobre el suelo) es la sombra Vs de V.
Siguiendo la dirección r' construimos las tangentes a la circunferencia base del cilindro obteniendo dos puntos diametralmente opuestos en la circunferencia (P' y otro punto que está detrás y no se ve, que es intersección de V1-P' con la circunferencia) por los que levantamos verticales, estas dos líneas verticales separan la luz de la sombra en el cilindro.
Si trasladamos la circunferencia superior del cilindro mediante paralelas a la recta r obtenemos la sombra de esta circunferencia, desde Vs hacemos las tangentes a esta circunferencia teniendo los puntos Ss y Ls que corresponden a las sombras de S y al otro punto que no se ve en la base del cono. Estos puntos unidos con el vértice del cono V delimita la línea separatriz entre luz y sombra de la figura.
Como podemos observar en las dos figuras, el cilindro y el cono, las líneas de separación entre la luz y sombra no son coincidentes, o lo que es lo mismo, P y S no coinciden en un único punto. Sólo se da esta peculiaridad en distintas superficies cuando son perfectamente tangentes, como el cilindro y el cono no lo son, no coinciden.
En la figura podemos ver el ejercicio resuelto en sistema diédrico:
Tenemos la dirección del rayo de luz en planta (r') y en alzado (r). En la planta seguimos esa dirección -r'- por el vértice en planta (V1). Igualmente en el alzado por el vértice V2 seguimos la dirección del rayo de luz correspondiente al alzado (por V2 hacemos la recta r hasta que corta la línea de tierra en Vs2, punto por el que hacemos una línea vertical que corta a la línea anterior r' en Vs1). Esta es la sombra Vs1 del vértice del cono en planta.
Por el mismo procedimiento trasladamos la sombra de la cara superior del cilindro obteniendo la circunferencia del centro N1 (es una circunferencia que tiene el mismo radio que las del cilindro y de la que sólo necesitamos calcular la sombra del centro de la cara superior, añadiendo el mismo radio podemos dibujar la circunferencia).
Desde la sombra del vértice,Vs1, en planta hacemos las tangentes a la circunferencia que determinan las sombras de los puntos que separan la zona entre luz y sombra del cono (Ss1 por ejemplo), por tanto haciendo paralelas a la dirección del rayo de luz en planta por estos puntos obtenemos en el corte con la circunferencia correspondiente al cono en planta dos puntos de intersección que corresponden a la separación entre la luz y sombra de la figura (S1 y su simétrico respecto a r'). Subimos estos puntos al alzado y obtenemos también la separación entre luz y sombra en el cono en el alzado.
En el caso del cilindro es más fácil, las tangentes comunes a las dos circunferencias en planta delimitan puntos de contacto con la circunferencia de la base del cilindro ( P1 y su simétrico respecto a r'), puntos que también subimos a la vista en alzado (P2), por estos puntos se trazan las verticales que separan la luz de la sombra en el cilindro en su vista en alzado.
Para calcular la sombra de la pirámide se determina la sombra As del vértice A como intersección del rayo de luz y su proyección ortogonal sobre el suelo. Unimos a continuación los vértices de la base con As, las líneas límites delimitan la sombra arrojada de la figura y sus puntos de contacto hasta el vértice A determinan la sombra propia.

Tenemos la dirección del rayo en el alzado y en planta su proyección, observamos en el alzado que el rayo de luz corta al suelo en P, bajamos una vertical hasta que corte a la proyección del rayo en planta en As. Unimos As con los vértices de la base y observamos los bordes de la sombra que delimitan 2 caras con sombra propia y las reflejamos también en el alzado.

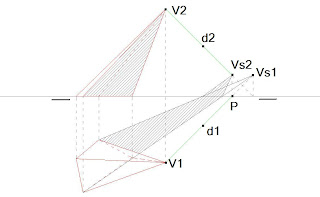
La sombra de una pirámide oblicua tiene un proceso afín al anterior, se calcula la intersección de la dirección de la luz d con el plano vertical que pasa por V y su proyección ortogonal V1 y el plano verde: su intersección es una vertical que pasa por P, punto de intersección del plano horizontal y vertical. La intersección de esta vertical y la recta d es la sombra de V, Vs2.
Desde Vs1, sombra de V sobre el plano horizontal si no hubiera plano vertical, se trazan las líneas del contorno de sombra y donde cortan a la intersección del plano vertical y horizontal se unen con Vs2.

En diédrico tenemos que calcular las trazas de la recta o rayo de luz d. La traza horizontal y vertical son respectivamente la sombra sobre el plano horizontal (Vs1) y vertical (Vs2).
La sombra de un prisma recto de base rectangular se obtiene trasladando la cara superior hasta llegar al suelo, por estar la cara y su sombra en una correspondencia llamada homotecia afín. Como la cara es paralela al suelo bastará con re-dibujar el rectángulo a partir del punto As y hacer las tangentes a los 2 rectángulos, la base y la sombra proyectada.

Uniendo los dos rectángulos idénticos tenemos la sombra arrojada completa en planta. Las dos caras sombreadas las marcamos a continuación sobre el alzado.

Para calcular la sombra de una figura plana ABC formada por varios puntos se calcula la sombra de cada punto sobre el plano horizontal Sa Sb Sc y sobre el plano vertical S’a S’b S’c.
La intersección de los dos triángulos sobre los dos planos es la línea en la que la sombra pasa del plano horizontal a vertical. La sombra de la figura está formada por los puntos del plano horizontal: Sa Sb y del vertical: S’c.

Para calcular la sombra en sistema diédrico por cada punto se proyecta la dirección de la luz en planta por cada uno de los puntos de la figura y en alzado se procede de la misma forma y en el momento en que estas líneas toquen la línea de tierra en dos puntos se hace una vertical por ambos, donde corten a las dos direcciones de cada punto se tiene las trazas de cada recta o rayo.
Para saber si corta en el plano vertical u horizontal, esto es, sobre que plano se proyecta la sombra, basta con saber que lo hace en el punto más cercano al punto de donde sale la luz, sea planta o alzado.

----------------------------------------------
Calcular la sombra que proyecta el prisma sobre la cuña:

Tenemos la dirección del rayo de luz en color amarillo y su proyección ortogonal sobre el suelo en color rojo, estos dos elementos determinan un plano vertical que contiene al rayo de luz y a la intersección del plano vertical con el suelo. Si prolongamos b' hasta que corte a la prolongación de la arista marrón, obtenemos P.
Por donde b' corta al plano vertical de la cuña levantamos una línea vertical b'' que es la sombra de un fragmento de b. Esta línea vertical corta al plano en pendiente en un punto que unimos con P. La intersección de esta recta con el rayo de luz amarillo determina el punto T. Si unimos este punto, el más alto de b'' con T, obtenemos la sombra del fragmento vertical que nos faltaba. Por T hacemos a continuación una línea verde horizontal que corresponde a la sombra de a.
-----------------------------------------
Tenemos un caso parecido al anterior con la diferencia de que el segmento vertical del prisma proyecta toda su sombra sobre el suelo y la pared vertical de la cuña, sin proyectarse como el anterior sobre el plano inclinado.

Tenemos el rayo de luz de color amarillo y su proyección sobre el suelo en color rojo, donde la proyección roja corta a la arista de la base del plano vertical de la cuña, levantamos una vertical hasta que intercepte al rayo amarillo en A', ésta es la sombra de este punto y por tanto la sombra del segmento vertical es la línea roja hasta el plano vertical y el segmento vertical PA'.
Como la sombra de la arista horizontal del prisma AN va a ser otra línea horizontal sobre el plano inclinado, por la intersección de los planos verticales de ambos elementos (el prisma y la cuña) hacemos una recta que prolongamos hasta que corta a la línea horizontal del prisma en el punto N. Unimos N con A' obteniendo en la intersección con la línea de pendiente del prisma el punto S. Por S hacemos una recta horizontal -en color verde- que es la sombra de la línea horizontal que pasa por AN.
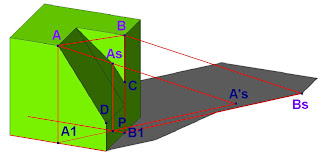
La sombra de la figura se calcula de la siguiente forma:
Tenemos la dirección A-As del rayo de luz y la dirección de su proyección C-B sobre el plano horizontal.
Como AB es un segmento vertical proyectará una sombra vertical As-C sobre un plano vertical. Levantamos en consecuencia una vertical por el punto C, intersección de la recta BC con la cara que pasa por el punto. Donde la vertical por C corte a la dirección A-As tenemos calculado As. La sombra de F-A será F-As, la de A-E será C-E. La sombra proyectada m es paralela a C-B por ser los planos que las contienen paralelos.

Para calcular la sombra del punto A hacemos una vertical para obtener en la intersección con la arista de la base, A1. Tenemos las direcciones de la luz A-As y su proyección A1-A’s.
Por B1, proyección de B, construimos la cara imaginaria paralela a A-A1-D, que intercepta a A1-A’s en P, levantamos por este punto una vertical hasta que corte a la dirección A-As en As, y esta es la sombra de A.
La sombra de AD es una paralela por As a la recta.
VÍDEO SOBRE CÁLCULO DE SOMBRAS EN UNA ESFERA CON LUZ DISTANTE
La sombra de una esfera se calcula por el cilindro tangente a la misma, la circunferencia ABCD es la circunferencia que separa la luz de la sombra.
La intersección del cilindro con el suelo es la sombra de la esfera As Bs Cs Ds.
Por el centro de la esfera pasa el eje del cilindro y corta en el plano del suelo en el centro de la elipse O’.

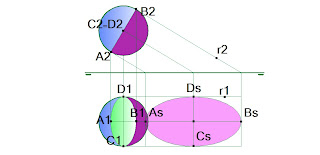
Para calcular en sistema diédrico la sombra propia y arrojada de la esfera, se dibujan las tangentes a la esfera en planta y alzado siguiendo la dirección r2 de los rayos de luz, en el alzado unimos los dos puntos de tangencia A2 B2 obteniendo la separación de luz y sombra -en violeta- y bajamos esos dos puntos a la planta A1 B1 y obtenemos el eje menor de la elipse, el mayor pasa por el centro de la esfera y es tangente a la misma en D1 C1.
En el alzado por el centro de la esfera seguimos la dirección del rayo r2 hasta que intercepta la línea de tierra en un punto por el que bajamos una vertical. En la planta seguimos la dirección de r1 por el centro de la esfera hasta que corte a la vertical anterior obteniendo así el centro de la elipse. La dirección de los rayos de luz en el alzado definidos por la recta r2 interceptan en la línea de tierra puntos por los que bajamos verticales que interceptan a las rectas horizontales por la dirección r1. La intersección de las horizontales y verticales nos determina el cuadrilátero donde se inscribe la elipse que es la sombra arrojada de la figura.
VÍDEO SOBRE CÁLCULO DE SOMBRAS EN UNA ESFERA CON LUZ PUNTUAL

Dada una esfera, determinar la sombra propia y arrojada sobre el suelo en el que se apoya por una luz puntual.
El cono de luz puntual tangente a la esfera divide a la misma en dos zonas, la correspondiente a la luz y la correspondiente a la sombra, la línea de tangencia que separa la luz de la sombra se le llama separatriz.
La intersección de ese cono con el plano del suelo produce una elipse que es la sombra que arroja la esfera sobre el suelo. En la esfera, la línea separatriz que separa la luz de la sombra es una curva plana de la misma, por tanto es una circunferencia homóloga de la sombra elíptica que proyecta la esfera sobre suelo.
http://homologias.blogspot.com/
 Para calcular en planta y alzado la sombra propia y arrojada de la esfera, hacemos en el alzado desde el punto de luz L1’ dos líneas tangentes a la esfera hasta que cortan a la línea de tierra en dos puntos N2 S2, que bajamos hasta la línea que une el centro de la esfera con el punto de luz en planta L1’, este segmento N1 S1 corresponde al eje mayor en planta de la elipse de la sombra proyectada de la esfera.
Para calcular en planta y alzado la sombra propia y arrojada de la esfera, hacemos en el alzado desde el punto de luz L1’ dos líneas tangentes a la esfera hasta que cortan a la línea de tierra en dos puntos N2 S2, que bajamos hasta la línea que une el centro de la esfera con el punto de luz en planta L1’, este segmento N1 S1 corresponde al eje mayor en planta de la elipse de la sombra proyectada de la esfera.Las dos tangentes en el alzado desde la luz L2’ definen los puntos de tangencia L2 T2 con la circunferencia del alzado, es el segmento separador entre luz y sombra sobre la esfera en el alzado, proyectamos estos puntos de tangencia sobre la planta obteniendo sobre la esfera el eje menor de la elipse L1 T1.
El cono tangente a la esfera lo es a la sombra elíptica proyectada sobre el suelo, por lo que los puntos de tangencia J1 Y están alineados con el punto de luz L1’ (como K1 D L’1).
El eje mayor de la elipse en planta (correspondiente a la circunferencia que separa la luz de la sombra propia de la esfera), es igual a la longitud en el alzado L2 T2 y es un segmento que pasa por el centro de la esfera, ambos segmentos están en verdadera magnitud, uno en planta y otro en alzado.
Si unimos los puntos del alzado N2 S2 correspondientes a la sombra proyectada de la esfera, y cogemos el punto medio O2 de ese segmento y lo unimos con el punto de luz L2’, obtenemos en la intersección con la línea L2 T2 el punto P2. Este punto lo bajamos a la planta y obtenemos la línea homóloga por P1 correspondiente a la que va ser la sombra del eje menor de la elipse H1 Ñ1. Unimos el punto el punto P1 que el punto L1’ de luz en planta y en la intersección de la vertical que pasa por el centro de la elipse en planta O1 correspondiente a la sombra proyectada tenemos H1, su simétrica Ñ1 determina la longitud real del eje menor H1 Ñ1 de la elipse.
Para calcular la sombra de una pieza que tenga planos en pendiente con elementos sobre ella, partimos de que la sombra del punto Z es Zs. Este es la dirección del rayo de luz por lo que el centro de la circunferencia del cilindro seguirá esta dirección y proyectará su sombra en la intersección de esta recta con la línea m, que es la proyección de equis sobre el plano en pendiente. Tenemos así que la sombra del punto O es Os. Se hacen las tangentes al cilindro (n) y definen la línea que separa la luz de la sombra.

La sombra del punto a se obtiene al hacer el plano vertical que pasa por la recta A -A1, la dirección del rayo de luz es A-As y la intersección del plano vertical con el prisma en pendiente en forma de cuña es A1-G. Por lo tanto la intersección de la recta con el plano en pendiente es As.
Para obtener la sombra arrojada ÑU sobre el plano vertical tenemos que la recta b corta a la recta a en el punto U. Tenemos por tanto que la sombra de la recta b es bs.

Tenemos la dirección del rayo de luz A-As y su proyección sobre el plano del suelo A1-As. Para saber dónde intercepta el rayo de luz que pasa por el punto B al plano rojo en pendiente calculamos la intersección del rayo de luz m con la recta de intersección del plano vertical que pasa por m y el plano en pendiente. El plano vertical corta al prisma rojo según la recta CE, ya que por el suelo lo corta según la recta ED y a partir del punto D hacemos una vertical DC hasta que corta al arista superior. La recta EC es la intersección del plano vertical con el plano en pendiente y corta a la recta m en el punto Bs, por lo tanto esta es la sombra del punto B.
Si por As tratábamos la paralela a la recta AB para proyectar la sombra de ella ahora tenemos que esta recta intercepta al prisma en un punto, este punto lo unimos con Bs y a partir de este punto hacemos como sombra una paralela a la arista superior del cubo ya que ésta es paralela al plano que está en pendiente.

Tenemos la dirección del rayo de luz en el espacio Q-Qs con su proyección sobre el suelo Q’-Qs. Hacemos un triángulo semejante que pase por los puntos A-A’y de esta forma obtenemos As, que es la sombra del punto A sobre el plano vertical. Haciendo una vertical por As obtenemos en el suelo de la pieza el punto P, que unido a A’nos da la dirección en el suelo de la sombra de A-A’. El punto As lo unimos con M y obtenemos en la arista el punto U por el que hacemos una paralela a la recta AM. Como el plano que contiene al punto U tiene pendiente, prolongamos la recta ZM hasta que corte a la recta n en el punto G. La intersección de la recta paralela a AM que pasa por U con la dirección del rayo de luz A-As intercepta la sombra del punto M, que es el punto T. Uniendo el punto T con G obtenemos en la intersección con la arista de la pieza el punto K.

La sombra de la circunferencia que pasa por el punto M. será otra circunferencia del mismo tamaño que pasa por el punto Ms. La sombra del punto B es Bs y ésta es la dirección del rayo de luz. Por el punto Bs hacemos una paralela a la recta BC hasta que intercepta al arista de la base en el punto I, éste lo unimos con A obteniendo en la arista de la pieza el punto P porque hacemos una paralela a la dirección de la proyección del rayo de luz, esto es, a la que pasa por el suelo y por Bs. Esta dirección por el punto P intercepta a la dirección del rayo de luz en el punto As por el que hacemos una paralela a la recta AU para tener la proyección de la sombra de esa arista.

Tenemos la dirección del rayo de luz que pasa por el punto A y su proyección m sobre el suelo a partir del punto A’.
La recta m corta a la traza del plano vertical en el punto P por donde se levanta una vertical que intercepta a la dirección del rayo de luz en el punto As. Se trata de calcular la sombra arrojada de la recta DJ sobre el cono. El plano que pasa por esa recta y que lleva los rayos de luz es un plano vertical que corta al cono según una hipérbola. Para determinar los puntos de la hipérbola se pasan planos verticales por el eje del cono OO’, que corta al plano vertical mencionado según la línea vertical que define un punto de la hipérbola que en su intersección con OZ. La sombra es por tanto una hipérbola que pasa por el punto L. Para calcular la sombra del segmento BD se procede de igual forma, por cada uno de los dos puntos se traza la dirección de los rayos solares que determinan un plano, si este plano corta a todas las generatrices del cono, como parece percibirse intuitivamente, estamos ante una curva elíptica y el ejercicio se reduce a calcular una sección del cono por ese plano.
En cuanto a la sombra del cono basta con calcular la sombra Os del vértice superior O, que es la intersección del rayo de luz por el espacio y su proyección sobre el suelo y desde ese punto trazar las tangentes t1 t2 a la base del cono. En los puntos de tangencia T1 T2, se trazan dos generatrices que vayan hasta el punto O, éstas son las líneas que separan la zona de luz y de sombra del cono.

La sombra de un punto cualquiera B de la circunferencia se calcula pasando un plano vertical por B hasta que corte al plano vertical de la pieza en Bs. Para calcular dónde empieza la elipse que pasa por el punto calculado hacemos la sombra del punto A que es el plano que contiene a los rayos de luz, esto es, la separación entre la luz y sombra del cilindro. La sombra del punto A es As y a partir de este punto empieza la curva elíptica que pasa por el punto Bs. Para calcular la sombra de la base superior del cono proyectamos el centro de la circunferencia O sobre un plano imaginario que esté a la altura de la cara superior del prisma, obteniendo el punto O1. Por éste. Trazamos la dirección del rayo de luz por el suelo y son de corte a la dirección del rayo de luz por el espacio O Os obtenemos la sombra del centro de la circunferencia. Trazamos otra circunferencia con el mismo horario y ya tenemos la sombra de la cara superior proyectada sobre la cara superior del prisma. La circunferencia corta a la arista del prisma en un punto por donde pasa la sombra elíptica de la cara vertical.

La sombra de un prisma sobre un plano inclinado la calculamos como en los ejercicios anteriores. Trazamos un plano vertical que pase por la recta AA’, este plano vertical intercepta a la pieza si la continuamos de forma imaginaria en la base en los puntos OP, por ambos levantamos una vertical hasta que corte a las aristas del plano en pendiente en los puntos M N. La recta que determinan éstos M N es la intersección del plano vertical con el plano en pendiente y la sombra del punto A se obtiene mediante la intersección As del rayo de luz que pasa por A y la recta MN. Los demás puntos Se calculan de igual forma, si prolongamos la recta AB y la recta As-Bs del plano en pendiente se cortan en un mismo punto del plano ya que ambas rectas pasan por el plano que contiene a los rayos de luz.
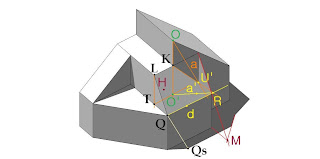 En este dibujo la dirección de los rayos de luz tiene determinada por la recta a y su proyección ortogonal sobre el suelo imaginario de la pieza por la recta a’.
En este dibujo la dirección de los rayos de luz tiene determinada por la recta a y su proyección ortogonal sobre el suelo imaginario de la pieza por la recta a’.Para calcular la sombra del vértice O de la pieza sobre el plano inclinado H, pasamos un plano vertical por O, tenemos que éste plano vertical corta al plano H según la recta RK. La intersección de esta recta con la dirección de la luz a nos determina la sombra U’ del vértice O.
 Se trata de determinar la sombra del segmento a sobre el plano inclinado con luz distante, de dirección de la luz c conociendo la sombra D del vértice superior R de este segmento a sobre el plano horizontal del suelo.
Se trata de determinar la sombra del segmento a sobre el plano inclinado con luz distante, de dirección de la luz c conociendo la sombra D del vértice superior R de este segmento a sobre el plano horizontal del suelo.Pasamos un plano vertical Rn por el vértice superior R del mismo. La proyección perpendicular v de este punto R sobre el suelo es el punto X, que unido con D obtenemos en la intersección con b el punto P. Si unimos los puntos PA (este punto A es la intersección de la recta vertical v que pasa por el punto X con el plano inclinado de la pieza) obtenemos en la intersección con el rayo de luz c la sombra T del vértice superior R del segmento a, que era lo que se quería calcular (intersección de las rectas m c). De esta manera la sombra as del segmento a pasará por este punto calculado y por el pie del segmento a. La sombra del segmento a será el segmento TU. La sombra del segmento superior que pasa por el punto R será una recta paralela por el punto T.
 Para calcular la sombra del segmento vertical a de la pieza sobre el plano inclinado adyacente, tenemos que las dos aristas a b de la pieza se cortan en un punto que llamaremos D como tenemos que la sombra del segmento vertical sobre el suelo es la recta c que intercepta al plano inclinado de la pieza en el punto Y, uniendo el punto D con Y tenemos la sombra n de la arista a sobre el plano inclinado.
Para calcular la sombra del segmento vertical a de la pieza sobre el plano inclinado adyacente, tenemos que las dos aristas a b de la pieza se cortan en un punto que llamaremos D como tenemos que la sombra del segmento vertical sobre el suelo es la recta c que intercepta al plano inclinado de la pieza en el punto Y, uniendo el punto D con Y tenemos la sombra n de la arista a sobre el plano inclinado.La dirección del rayo de luz en el espacio viene determinada por la recta r, por lo que si pasamos un plano vertical por esta recta, tenemos que su traza horizontal c corta a la traza horizontal v del plano en un punto G por el que hacemos la recta intersección h que es vertical por ser los dos planos verticales. La intersección del plano en pendiente con el plano hc es la recta i, que es la sombra del segmento vertical MB de la pieza. La intersección de las dos rectas i r nos determina la sombra Ms del punto M de esa arista.
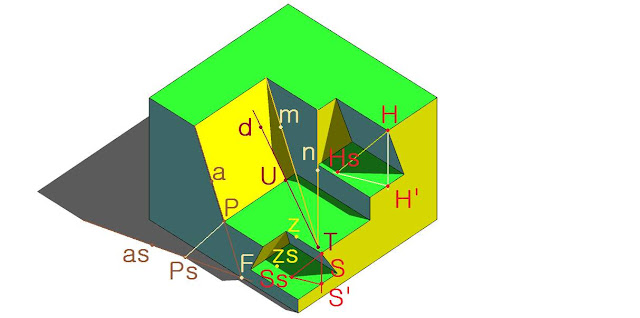 Tenemos un punto H, su proyección ortogonal sobre un plano horizontal H’, y la dirección del rayo de luz H-Hs.
Tenemos un punto H, su proyección ortogonal sobre un plano horizontal H’, y la dirección del rayo de luz H-Hs.Si queremos calcular la sombra del segmento vertical n sobre el plano inclinado amarillo, tenemos que este segmento n se proyecta sobre el plano horizontal verde siguiendo la dirección Hs-H’ hasta interceptar al plano inclinado en el punto U. Si prolongamos las rectas m n (aristas de la pieza) hasta que se corten en el punto T, tenemos que la sombra d del segmento n pasa por los puntos TU.
Haciendo triángulos proporcionales por cada uno de los puntos de la figura, obtenemos los puntos de sombra respectivos, de esta forma haciendo un triángulo proporcional al primero H-Hs-H’ por T tenemos el triángulo T-S’-Ss. De esta manera la sombra del segmento TS será el segmento S-Ss. Tenemos además que la sombra del segmento z será el segmento zs, por ser planos paralelos. Donde el segmento zs intercepte al plano amarillo inclinado menor lo unimos con el punto final del segmento z, obteniendo la sombra arrojada de este último.
Para calcular la sombra del segmento inclinado a lo prolongamos hasta que corta a la base de la pieza en el punto F, por este punto seguimos la dirección H’-Hs y obtenemos la sombra as del segmento a. La sombra Ps del punto P se obtiene en la intersección de la dirección del rayo de luz que pasa por P con la línea as.
Para calcular la sombra de la figura empezamos por el rectángulo amarillo, tenemos la dirección p del rayo de luz y su proyección sobre un plano horizontal TX, seguimos esa dirección por la proyección T del punto A sobre la referencia del plano horizontal rosa sobre el que vamos a calcular la sombra, seguimos la dirección del rayo sobre el suelo hasta que intercepta en el plano rosa el punto As. La dirección del rayo por el suelo T-As determina en la arista de la cuña verde el punto X, lo unimos con la proyección B de A sobre la cuña.
Por As hacemos una recta paralela a la dirección d, que es una de las direcciones de las aristas de la pieza hasta interceptar en el plano azul el punto Y, punto que unimos con el vértice superior del rectángulo amarillo, construyendo la dirección m proyectada de la sombra sobre un plano vertical.
Esta dirección nos va a servir para calcular la sombra del cuerpo cilíndrico, ya que por el centro de la circunferencia roja hacemos una recta paralela m' a m y donde cortae a la circunferencia trazamos la dirección d hasta obtener con la circunferencia de fuera el punto I, por éste, hacemos una paralela p' a la dirección del rayo de luz p. Este rayo de luz por I intercepta a m' en el punto Is, por donde pasa una circunferencia de igual tamaño a la del cilindro, una circunferencia idéntica a la de fuera que hemos desplazado según la dirección I-Is hasta el plano rojo. Esta circunferencia que separa la luz de la sombra en la zona roja intercepta a la pared del cilindro en el punto K. Si hacemos por la circunferencia exterior del cilindro, la que queda sobre la pared azul, una línea paralela tangente por L a la recta m tenemos el punto por el que va a pasar una curva LK, que es la sombra de la curva sobre el cilindro.
En la figura tenemos un prisma con las paredes tan delgadas que resultan despreciables en el dibujo, podría ser una caja de cartón, se pide calcular la sombra que proyecta la figura sobre las caras, sabiendo que la sombra del punto A es As.
Si bajamos verticales por ambos puntos obtenemos los nuevos puntos que aparecen sobre las aristas inferiores de la caja, obtenemos la proyección del rayo de luz r sobre el suelo, que es r'.
A partir de aquí todas las sombras de cada punto la podemos obtener por este método, por ejemplo por los puntos B y Ñ trazaremos dos líneas m y c paralelas a la dirección del rayo de luz r, mientras que por la proyección ortogonal R sobre la base de la caja trazaremos una recta a cuya dirección coincide con la proyección del rayo de luz sobre el suelo, esto es, r'. De esta manera obtenemos en la intersección con c y m, al levantar una vertical por Q los puntos J y Bs, que son las sombras de Ñ y B, respectivamente.
La sombra de AB será una paralela por As hasta que intercepta la arista opuesta vertical de la caja, éste punto lo unimos con Bs obteniendo la dirección de la recta que haremos también por J hasta el vértice de la cara naranja.
A la izquierda uniremos As con H, obteniendo la sombra de la arista superior del rectángulo rojo.
 para calcular la sombra del detalle de la izquierda de la pieza, de la que se sabe la dirección del rayo de luz distante v y su proyección sobre el suelo z, prolongamos la recta a hasta que corta en el suelo a la prolongación de la recta e en el punto P.
para calcular la sombra del detalle de la izquierda de la pieza, de la que se sabe la dirección del rayo de luz distante v y su proyección sobre el suelo z, prolongamos la recta a hasta que corta en el suelo a la prolongación de la recta e en el punto P.La recta as que pasa por P y por la intersección del rayo de luz v y su proyección sobre el suelo z intercepta al plano vertical adyacente en el punto K. Si K lo unimos con Y, tenemos la sombra del segmento a sobre un plano vertical (siendo Y la intersección de la recta f de las dos caras de la figura con la recta a). Esto quiere decir que sobre un punto cualquiera de un segmento de la pieza podemos hacer rectas paralelas a esta dirección (como la recta b) para obtener la sombra de ese punto S, siempre y cuando estemos sobre planos verticales paralelos al anterior. De esta forma hemos calculado la sombra arrojada g de la arista T sobre el plano cilíndrico. Para determinar la sombra del vértice W hacemos una recta paralela r al rayo de luz v hasta que intercepte a la línea separatriz g obteniendo de esta forma su sombra que es el punto K.
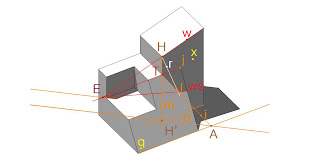 Para calcular la sombra de una cara x de la figura sobre el plano en pendiente q, tenemos que H tiene su proyección ortogonal sobre el suelo H’, la dirección de la luz viene determinada por la recta r, su proyección ortogonal sobre el suelo viene definida por la recta n. La intersección del plano en pendiente g y el plano vertical que pasa por la recta m es la línea TA (la que determinan dos trazas de los planos). La intersección de esta recta con el rayo de luz r determina la sombra del punto H sobre el plano inclinado, que es I.
Para calcular la sombra de una cara x de la figura sobre el plano en pendiente q, tenemos que H tiene su proyección ortogonal sobre el suelo H’, la dirección de la luz viene determinada por la recta r, su proyección ortogonal sobre el suelo viene definida por la recta n. La intersección del plano en pendiente g y el plano vertical que pasa por la recta m es la línea TA (la que determinan dos trazas de los planos). La intersección de esta recta con el rayo de luz r determina la sombra del punto H sobre el plano inclinado, que es I.Si prolongamos la recta Hw hasta que corte a la recta TJ en el punto E, y pasamos una recta por E y el de la sombra del punto I obtenemos la sombra arrojada del segmento HW sobre el plano inclinado g, que es la recta I-ws. Esta recta es la sombra de la lista de la figura definida por los puntos HW.
 Para calcular la sombra del cono apoyado en una generatriz, calculamos la sombra de cada punto de la circunferencia de la base por el procedimiento ordinario, esto es, unimos cada uno de los de la circunferencia con el punto de luz y dónde intercepta con el plano del suelo la proyección ortogonal del rayo de luz tenemos la sombra de ese punto (es la intersección de la traza del plano vertical que pasa por el punto de luz y el rayo de luz).
Para calcular la sombra del cono apoyado en una generatriz, calculamos la sombra de cada punto de la circunferencia de la base por el procedimiento ordinario, esto es, unimos cada uno de los de la circunferencia con el punto de luz y dónde intercepta con el plano del suelo la proyección ortogonal del rayo de luz tenemos la sombra de ese punto (es la intersección de la traza del plano vertical que pasa por el punto de luz y el rayo de luz).Una vez que tenemos la sombra de la circunferencia base del cono, que es por regla general una elipse, hacemos desde el vértice del cono V las rectas tangentes a esta elipse. Los puntos de tangencia T1 los unimos con el punto de luz L y donde cortan a la base del cono tenemos los puntos P (y el correspondiente al del otro lado) que unidos con el vértice V definen la línea separatriz que separa la luz de la sombra en el cono (la recta definida por P y el vértice del cono V es la que separa la luz de la sombra en la superficie). En la figura no se puede percibir claramente esta línea por ser el cono una superficie reflectante y mostrar con más fuerza las tonalidades del espacio circundante que las que corresponden a las zonas de luz y de sombra.
 En la figura podemos observar un toro con su sombra propia y su sombra arrojada sobre el suelo por luz distante, esto es, por rayos paralelos de luz.
En la figura podemos observar un toro con su sombra propia y su sombra arrojada sobre el suelo por luz distante, esto es, por rayos paralelos de luz.Para calcular ambas sombras, se hace una superficie cilíndrica cuyas generatrices sean tangentes a la superficie tórica. La curva que une los puntos de tangencia de ambas superficies define la zona que separa la luz de la sombra. La superficie cilíndrica corta al suelo según una curva que separa la luz de la sombra.
 Existe una esfera generatriz imaginaria que puede girar tangente dentro de la superficie del toro de manera que el cilindro tangente que la circunscribe definido por el rayo de luz determina una elipse en planta (proyección de la circunferencia separatriz) que hemos ubicado en el centro del toro. Cualquier radio Z prolongado hacia el toro de esta elipse marca los puntos de la separatriz Z y Z sobre el toro.
Existe una esfera generatriz imaginaria que puede girar tangente dentro de la superficie del toro de manera que el cilindro tangente que la circunscribe definido por el rayo de luz determina una elipse en planta (proyección de la circunferencia separatriz) que hemos ubicado en el centro del toro. Cualquier radio Z prolongado hacia el toro de esta elipse marca los puntos de la separatriz Z y Z sobre el toro.Para calcular en el sistema diédrico la sombra propia y arrojada de la figura dada en planta, hacemos el alzado y dibujamos en ambas vistas la dirección de los rayos de luz d1 d2. Como podemos observar en el alzado, la dirección de los rayos de luz tangente a la superficie intercepta al plano del suelo en los puntos Cs2, As2, Bs2. Estos puntos los bajamos hasta que cortan a la dirección de los rayos de luz en planta d1 por el centro de la figura en los puntos Cs1, As1, Bs1. Para calcular nuevos puntos de la sombra arrojada del toro sobre el plano del suelo hacemos secciones por planos verticales paralelos a la dirección de la luz d1, de esta manera obtenemos una curva de sección S llamada de Cassini, haciendo las rectas tangentes a esta curva en el alzado en la dirección de la luz d2 obtenemos la sombra de G, que es el punto Gs2 que proyectamos a la planta obteniendo en la intersección con la dirección de los rayos de luz por la curva S el punto Gs1.
Los puntos de tangencia al toro de la dirección de los rayos en el alzado defienden la curva separatriz entre luz y sombra en el alzado, estos puntos que separan la luz de la sombra los bajamos a la planta y dibujamos las curvas correspondientes a la sombra propia de la figura: el punto de tangencia en el alzado A2 definido por la dirección del rayo de luz lo bajamos sobre la planta obteniendo su proyección sobre el toro en el punto A1, en este punto empieza la línea curva por donde comienza la sombra propia n del objeto. Hacemos lo mismo con la parte exterior del toro, el punto C2 que determina la tangente en el alzado los bajamos a la planta y tiene su correspondiente sobre la dirección del sol d1. De igual forma la tangente en el alzado por el punto G2 de la curva de Cassini S2 define la recta azul i que es la línea que separa la luz de la sombra en el contorno exterior del toro.
 En la figura podemos observar la perspectiva de una pieza, la sombra arrojada de la misma coincide con el contorno de la pieza, ya que en este caso la dirección de los rayos de luz coincide con la dirección del punto de vista en el infinito, que es donde está el centro de proyección en una axonometría.
En la figura podemos observar la perspectiva de una pieza, la sombra arrojada de la misma coincide con el contorno de la pieza, ya que en este caso la dirección de los rayos de luz coincide con la dirección del punto de vista en el infinito, que es donde está el centro de proyección en una axonometría. Si giramos directamente la perspectiva axonométrica de la pieza observaremos que efectivamente la sombra coincidía con el contorno de la misma. Como ahora la sombra y la figura ya no son coincidentes, las dimensiones y la forma de la sombra arrojada difieren de las dimensiones y el contorno de la pieza.
Si giramos directamente la perspectiva axonométrica de la pieza observaremos que efectivamente la sombra coincidía con el contorno de la misma. Como ahora la sombra y la figura ya no son coincidentes, las dimensiones y la forma de la sombra arrojada difieren de las dimensiones y el contorno de la pieza. En la figura observamos cómo se proyecta la circunferencia base del cilindro hueco sobre la superficie cilíndrica por la parte inferior de la superficie.
En la figura observamos cómo se proyecta la circunferencia base del cilindro hueco sobre la superficie cilíndrica por la parte inferior de la superficie.Por un lado tenemos la dirección de los rayos de luz P-Ps por los que se pasan planos verticales que interceptan a las direcciones Ps-M coincidentes con las generatrices de la superficie cilíndrica en los puntos de sombra Ps, que son los puntos de intersección de cada rayo de luz a y su proyección vertical sobre el cilindro Ps-M.
A partir del segmento horizontal b que pasa por el centro de la circunferencia, es donde empieza la línea separatriz entre luz y sombra.
 En la figura podemos observar la sombra de P de la cara superior sobre el suelo Ps2, por Ps2 se hace una paralela g a la arista determinada por los puntos N P obteniendo la sombra de esa arista.
En la figura podemos observar la sombra de P de la cara superior sobre el suelo Ps2, por Ps2 se hace una paralela g a la arista determinada por los puntos N P obteniendo la sombra de esa arista.Podemos observar que la dirección de los rayos de luz por el espacio viene definida por P y su sombra sobre el suelo Ps2. Por lo tanto la proyección del rayo de luz sobre el plano horizontal viene determinada por la recta d. Si por Ps2 hacemos una recta perpendicular a la cara NPW, tenemos que en el punto de intersección con W unido con P, la dirección por la que obtenemos la sombra sobre el cilindro de la arista NP y que pasa por el punto Ps1.
Por el punto Ps2 hacemos un plano perpendicular a la cara de la figura que define la recta w y el punto P. De esta forma obtenemos la sombra Ps1 del punto P sobre el cilindro, basta con hacer la generatriz del cilindro por el punto de intersección de la recta amarilla de la cara de la figura con la base del cilindro. Donde esta generatriz corta a la recta determinada por los puntos P-Ps2 obtenemos la sombra Ps1 del punto P sobre el cilindro.
Para calcular otros puntos procedemos de igual forma, por el punto N hacemos dos rectas paralelas al triángulo amarillo anterior hasta que corten a la generatriz que pasa por el triángulo nuevo, obteniendo de esta forma un nuevo punto de sombra Ns de la arista NP sobre el cilindro.
 Pasando triángulos por la arista vertical y horizontal de la figura obtenemos en la intersección con las generatrices respectivas del cilindro, la sombra arrojada de estos dos segmentos. En realidad lo que se está haciendo aquí es pasar planos todos paralelos al primero en el que se calculó de la recta de luz r su proyección ortogonal d sobre la cara de la figura.
Pasando triángulos por la arista vertical y horizontal de la figura obtenemos en la intersección con las generatrices respectivas del cilindro, la sombra arrojada de estos dos segmentos. En realidad lo que se está haciendo aquí es pasar planos todos paralelos al primero en el que se calculó de la recta de luz r su proyección ortogonal d sobre la cara de la figura.Como tenemos que la luz es distante, la sombra del cilindro afectará a la mitad de su superficie, por lo que tenemos que si en B, la línea separatriz de luz y sombra es la recta Ms que es la tangente a la circunferencia, la línea separatriz por el otro lado del cilindro, pasará por A, diametralmente opuesto al anterior B, para calcularlo bastará con unir el punto B con el centro O de la circunferencia por donde pasa el eje del cilindro y prolongarlo hasta que corte a la circunferencia en el punto A. A continuación calculamos la sombra del segmento AB, su sombra arrojada genera la curva elíptica a partir de estos dos puntos As Bs.
Las sombras a b de cualquier recta de un objeto en perspectiva cónica siguen los principios perspectivos de la misma, al igual que las líneas paralelas c d del objeto convergen en un punto por efecto de la perspectiva, las sombras de estas rectas por ser paralelas a ellas también concurren en el mismo punto de fuga.

Sombras propias y reflejos en una pieza son elementos usualmente inversamente proporcionales, esto quiere decir que cuanto más reflectante sea una pieza menos sombras propias va a mostrar. Un objeto enteramente reflectante construido con espejos como refleja lo que tiene alrededor no asume sombras. Hay objetos en los que las sombras y los reflejos están repartidos más o menos a un 50%, pueden ser objetos ligeramente reflectantes como una pieza de plástico o una piedra con cierto grado de pulimento. En la imagen observamos que allí donde se reflejan los detalles se van perdiendo la nitidez de los mismos en la profundidad de la pieza. También podemos observar que las sombras incrementan el efecto de la oscuridad de la reflexión. De igual forma cuanta más luz muestra el objeto, menos se perciben las sombras en él. La reflexión del prisma en forma de cuña se percibe en el plano vertical y horizontal pero deja de percibirse la reflexión de la reflexión. La sombra es más nítida cuando está más cerca del objeto por efecto de la difusión de la luz y las sombras del objeto también experimentan reflexión, por lo que hay que sumarlas a los tonos de la sombra.

Un punto de luz proyecta la sombra de una esfera sobre un plano. El contorno de esa sombra arrojada es más nítido cuanto más puntual será la luz. La figura se refleja sobre la sombra con más intensidad que sobre el resto del plano en el que se refleja con más fuerza la luz.

La penumbra es un efecto de la luz debido a que ésta no es puntual, cuanto más unidos estén los puntos de luz y más pequeña sea ésta, la penumbra será menor. Un punto de luz proyecta una sombra, otro punto de luz proyecta otra y la intersección de las dos sombras es una zona donde, en teoría, no llega luz ninguna y es la zona de sombra, excepto por un efecto atmosférico y por los fotones que rebotan produciendo ese efecto virtual llamado radiosidad.

http://sombras-en-perspectiva-conica.blogspot.com/
 Para calcular la sombra de una pieza con luz solar (rayos de luz considerados paralelos por la lejanía del sol), se toman los puntos de la misma A, B, C, D (vértices en color amarillo) y se obtiene de ellos en el pie de su perpendicular al plano del suelo la proyección ortogonal A’, B’, C’, D’ (en color azul). Por la proyección ortogonal de cada punto pasa la proyección del rayo sobre el suelo (en color rojo). La proyección del rayo de luz sobre el suelo donde se apoya la pieza es en realidad la intersección del plano vertical que pasa por el rayo de luz con el suelo y como los rayos de luz son paralelos, sus proyecciones sobre el suelo también lo son.
Para calcular la sombra de una pieza con luz solar (rayos de luz considerados paralelos por la lejanía del sol), se toman los puntos de la misma A, B, C, D (vértices en color amarillo) y se obtiene de ellos en el pie de su perpendicular al plano del suelo la proyección ortogonal A’, B’, C’, D’ (en color azul). Por la proyección ortogonal de cada punto pasa la proyección del rayo sobre el suelo (en color rojo). La proyección del rayo de luz sobre el suelo donde se apoya la pieza es en realidad la intersección del plano vertical que pasa por el rayo de luz con el suelo y como los rayos de luz son paralelos, sus proyecciones sobre el suelo también lo son.Por cada uno de los puntos de la pieza pasan los rayos de luz (en color amarillo). La intersección de los rayos de luz amarillos con sus proyecciones sobre el suelo de color rojo son la sombra As, Bs, de cada punto (en color verde).
Si una arista de la pieza está formada por dos puntos consecutivos AB, sus sombras As Bs también determinarán la sombra de la arista que pasa por esos dos puntos adyacentes. Si prolongamos la arista m de la pieza que pasa por esos dos puntos hasta que corta al suelo en un punto P, tenemos que la sombra ms de esa arista también pasa por ese punto P, ya que si la arista de la pieza continuara hasta el suelo, lógicamente la sombra saldría del punto P que se apoyaría en el suelo.
En consecuencia, para calcular la sombra de la pieza basta con hacer triángulos proporcionales o semejantes (triángulos de igual forma pero de distinto tamaño cuando la altura de cada punto es distinta) por cada uno de los vértices de la misma y a continuación unir los puntos correspondientes de su sombra arrojada con el mismo orden que están en la pieza. Hay que tener en cuenta que la sombra arrojada (la que se desprende sobre el suelo) es la que determina este procedimiento, hay que añadir a ésta una sombra propia del objeto que es aquella que yace sobre cada cara de la pieza a la que no llega la luz, además de otra sombra autoarrojada dentro de la pieza que resulta de la intersección de cada rayo de luz con cada cara de la pieza y para cuya resolución determinamos la intersección de una recta y un plano, la correspondiente al rayo de luz y al plano que intercepta.

Un punto de luz ilumina una esfera y provoca en ella una sombra propia y otra que arroja en el suelo. El punto de luz se refleja asimismo en el suelo mediante una simetría espacial. Existe otra simetría espacial, la que provoca el brillo sobre la esfera que queda definido por el rayo reflejado de la esfera de luz, que forma igual ángulo con el eje de simetría ortogonal a la esfera y a un plano tangente a la misma y el ángulo que forman el rayo de luz incidente sobre la esfera con el mismo eje.

El punto de luz es el vértice de un cono tangente a la esfera según una circunferencia denominada separatriz que separa la zona de luz y de sombra. Este cono oblicuo corta al suelo según una elipse que es la sombra de la esfera sobre el suelo.
Si dibujamos la proyección ortogonal del punto de luz sobre el suelo tenemos L’, a igual distancia por debajo del suelo tenemos la reflexión del punto L, que es el punto Lr.
Las tangentes a la esfera c d lo son también a la sombra elíptica de la esfera sobre el plano del suelo.
Si desde la proyección ortogonal sobre el suelo L’ del punto de luz L hacemos las tangentes a b a la sombra de la esfera, tenemos la proyección ortogonal del cono en planta.

Dada una esfera, su sombra propia y arrojada sobre el suelo y el lustre o brillo que produce un foco de luz del que no sabemos su posición, se trata de calcular la posición exacta del punto de luz así como de la esfera respecto al plano del suelo.
Se pide obtener la altura o cota del punto de luz y de la esfera respecto al suelo.
En principio, en muchos objetos, la posición relativa del punto de luz es proporcional a la altura del objeto, por ejemplo en un prisma podemos tener un punto de luz a poca altura y un prisma de poca altura y obtener cierta sombra. Si elevamos proporcionalmente el punto de luz y el prisma podemos obtener la misma sombra arrojada en planta, esto quiere decir que lo único que podemos obtener en planta es la posición o proyección en planta del punto de luz, pero no podemos determinar su altura, ni la del prisma. En algunos objetos es posible calcular su posición exacta, como en la esfera, debido a su sombra propia que aparece oblicua respecto al plano de planta. La sombra propia en la esfera queda separada de la luz por una circunferencia que se proyecta en planta como una elipse siempre perpendicular al eje de revolución del cono de luz circunscrito a la esfera.

Dada la esfera en planta y su sombra propia y arrojada, para determinar la posición exacta de la esfera respecto al suelo y el punto de luz, hacemos primero las tangentes s d a la sombra elíptica y a la esfera en planta obteniendo en su intersección la proyección en planta del punto de luz G.
Dibujamos la elipse que separa la zona iluminada y sombreada de la esfera en planta, es una elipse tangente a las dos rectas s d y perpendicular al eje del cono q en el alzado, cono que es tangente a la esfera. El eje mayor m de esta elipse en planta será igual al eje mayor de la elipse w en el alzado, es una elipse que se transforma en una recta w perpendicular al eje de revolución q del cono.
Si construimos cualquier proyección en alzado de la esfera y hacemos las tangentes r1 r2 a la elipse en planta por su eje menor, observamos que éstas cortan siempre a la esfera en dos puntos U C. También podemos proyectar la esfera en el alzado a cualquier altura y tomar el punto del cuadrante U de la elipse y a partir de él tomar el eje mayor del elipse m con un arco UC obteniendo así el punto C.
Por el centro de la esfera en el alzado P2 se hace una recta perpendicular q a la línea de separación de la luz y la sombra UC obteniendo en la intersección con la vertical que pasa por el punto G el punto
de luz L en alzado. Las tangentes a la esfera en el alzado pasan por los puntos U C y por el punto de luz L y tienen su base en la intersección Ñ H de las verticales f1 f2 por los extremos del eje mayor de la sombra elíptica en planta. En consecuencia por estos puntos Ñ H es por donde pasa el plano del suelo o la línea de tierra. Las tangentes a la esfera t1 t2 en el alzado tienen el mismo ángulo que las tangentes d s a la esfera en planta, ya que es el mismo cono circunscrito a la esfera en proyecciones distintas.
El brillo que aparece sobre la esfera K en el alzado (define el correspondiente a la planta) queda determinado por la dirección a, ésta es la dirección del rayo reflejado simétrica respecto al eje e ortogonal a la esfera por su centro P2, de manera que según las leyes de la reflexión, el rayo de luz a’ forma con el eje e el mismo ángulo que el rayo reflejado a con este eje e. Esta dirección a que refleja el punto de luz L sobre la vertical sólo se puede ver sobre el dibujo de la esfera en la planta, por lo que el lustre aparece en ella sobre la proyección en planta B del punto K, que es la intersección de la recta vertical a que pasa por el punto K con el eje de revolución del cono en planta G-P1.
Para calcular el brillo x del alzado habría que seguir el mismo procedimiento, sería siempre un punto de luz que quedaría sobre el eje de revolución q y cuya dirección del rayo reflejado quedaría definido por una recta de punta ortogonal al plano del alzado.
 Dada una esfera en planta y alzado, determinar la posición exacta del foco de luz que la ilumina sin tener en cuenta ninguno de los objetos que aparecen reflejados sobre ella, salvo la reflexión del punto de luz o lustre.
Dada una esfera en planta y alzado, determinar la posición exacta del foco de luz que la ilumina sin tener en cuenta ninguno de los objetos que aparecen reflejados sobre ella, salvo la reflexión del punto de luz o lustre.Como es una esfera cromada enteramente reflectante, no tiene sombra propia ya que refleja todo lo que está a su alrededor, refleja el espacio circundante en color negro, dos prismas en color azul y rosa y su sombra arrojada sobre el suelo y sobre el prisma azul. En el ejercicio se pide calcular la posición exacta del foco de luz en planta y en el alzado, partiendo de su reflexión sobre la esfera.

Tenemos que la reflexión del foco de luz sobre la esfera es el punto B1 B2 en planta y en el alzado, respectivamente. Hacemos una línea vertical d por B1 hasta la parte superior R2 de la esfera, que es donde se ve realmente sobre la planta.
Si por R2 hacemos una línea que pasa además por el centro de la esfera O2, tenemos el eje de simetría e del rayo de luz. Construimos la recta simétrica d’ del rayo de luz vertical y obtenemos en la intersección con la línea que pasa por el centro de la esfera O2 y la reflexión B2 en el alzado, el punto de luz en el alzado L2.
Para obtener el punto de luz en planta hacemos una línea que pasa por el centro de la esfera O1 y por R1. Donde esta línea corta a la vertical que pasa por el punto L2, obtenemos la proyección del punto de luz L2 en planta.
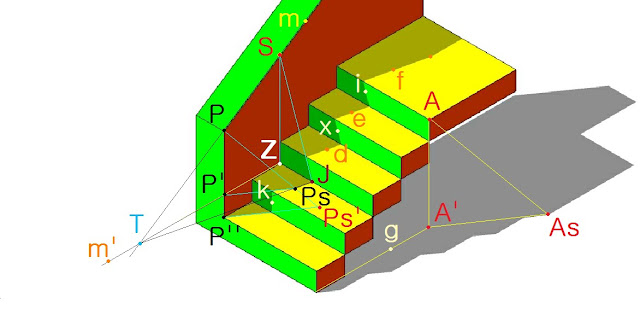
Para calcular las sombras de una escalera, tanto las propias como las que arroja sobre sí misma y sobre el suelo, se sigue el procedimiento usual: el punto A de la escalera tiene su proyección sobre el suelo en A’, la dirección del rayo de luz viene determinado por la dirección A-AS. La proyección de este rayo de luz viene determinado por la dirección A’-AS. La intersección del rayo de luz y de su proyección nos determina la sombra As del punto A.
Siguiendo en la misma línea tenemos que P y su proyección P’ sobre el plano del suelo en el que proyecta sombra, o sea la huella primera o primer escalón en su parte superior en color amarillo, tenemos por tanto a partir de estos dos puntos las dos direcciones, la que se determina sobre la huella amarilla del escalón P’’-Ps’, paralela a la dirección A’-As y la recta P-Ps’ paralela al rayo de luz. La intersección del rayo de luz y su proyección sobre la huella es la sombra Ps’ del punto P sobre ese plano, en caso de que no interfiriera con la primera contrahuella en sombra. Donde la proyección del rayo de sol interfiere con la contrahuella tenemos que la sombra del segmento P-P’’ es la línea k, ya que un segmento vertical se transforma en una recta de sombra vertical sobre un plano vertical.
Una vez que esta recta k toca a la segunda huella correspondiente al segundo escalón, por éste punto de intersección hacemos una recta paralela a la anterior P’’-Ps’, obteniendo así una recta que corta a la recta P-P’’ en el punto P’. Corta además a la recta P-Ps’ en el punto Ps. Ps es la sombra del punto P sobre la segunda huella de la escalera. (Las huellas son los planos horizontales amarillos de los escalones, las contrahuellas son los planos verticales de los escalones)
Si por el punto Z correspondiente a la huella segunda hacemos una prolongación de su arista tenemos que corta a la prolongación del pasamanos m en el punto T, que unido a Ps tenemos en su prolongación al punto J. Ps-J que es la dirección de las sombras del segmento m sobre los planos horizontales o huellas de los escalones.
Si por Z seguimos la dirección vertical de la tercera contrahuella tenemos que corta a m en el punto S, que unido con J nos define las sombras paralelas de las contrahuellas a partir de este escalón, de esta forma la recta SJ es paralela a la recta x y a la recta i. De la misma forma las rectas d, e, f son paralelas a la recta original Ps-J.

En la figura podemos observar el cálculo del ejercicio anterior en sistema diédrico. Tenemos la planta y el alzado de las escaleras así como el cambio de plano o proyección en perfil sobre el lateral izquierdo de la planta. Como sabemos la nueva línea de tierra lleva dos segmentos de cada lado y el giro de ese plano vertical nuevo de proyección, ortogonal al plano horizontal es de 90°, por lo que deja ver el perfil de los escalones y la pendiente de la línea (m) del pasamanos.
Podemos ver la dirección del rayo de luz en planta y alzado, viene determinado respectivamente por la línea A1-As1 y por la línea A2-As2. Como sabemos por el punto determinado por sus proyecciones A1 A2, se definen las dos proyecciones del rayo en planta y alzado, donde la proyección del rayo en alzado corta al plano del suelo (en As2) se baja una línea vertical hasta que corta a la dirección del rayo de luz en planta definido por la línea A1-As1, siendo este último punto la sombra en planta de A1.
Siguiendo la misma dirección en planta y alzado tenemos que por el punto P del pasamanos definido por sus dos proyecciones P1 P2 corta al rayo de luz en proyección vertical al segundo escalón en el punto Ps, tal y como se puede observar en el alzado. Ps lo bajamos a la planta hasta que corta a la dirección del rayo de luz en planta desde el punto P1, obteniendo de esta manera el punto Ps1.
La dirección del rayo de luz en planta por P1, intercepta a la segunda contrahuella en un punto con el que hacemos la sombra vertical sobre esta contrahuella.
En la proyección por cambio de plano del perfil de la escalera, en el lado izquierdo hemos abatido todos los elementos con sus dimensiones reales, de esta forma tenemos que la pendiente abatida del pasamanos corta al plano vertical que pasa por la segunda huella del segundo escalón sobre la línea e en el punto T. Para obtener las dimensiones reales en esta nueva proyección, tenemos que la distancia del alzado desde el punto P2 hasta el suelo, se repite sobre todas las huellas de los escalones, de esta forma tomamos esta medida y hacemos centro en el vértice Z2 definiendo una circunferencia que corta a la línea del pasamanos en el punto S2, esta distancia Z2-S2, es la que hemos puesto en el perfil abatido (S) (Z) para definir la pendiente alfa del pasamanos.
Este punto T se proyecta sobre la planta en la que prolongamos también la línea S1-P1 del pasamanos, cortando a la proyección del punto anterior en el punto T1. Al Unir Ps1 con T1 tenemos la dirección Ps1-J1 que se repite sobre todas las huellas de los escalones y es la que corresponde a la sombra de la arista m del pasamanos sobre esos planos horizontales de los escalones.
Sombras y reflexiones
Sombra de rectángulo vertical con luz puntual y distante en el espacio.
http://youtu.be/G4o2M_BTRYY
Sombra de cuadrado vertical en perspectiva cónica. Luz solar.
http://youtu.be/7zZ3SkIRXls
Sombra de círculo vertical. Cálculo de ejes principales.
http://youtu.be/rT2c-vNMlFY
Penumbra
http://youtu.be/VYUobHA9rjg
Sombra arrojada por un triángulo sobre los 2 planos de proyección del sistema diédrico.
http://youtu.be/e7s1J02opAQ
Sombra distante y puntual de un prisma
http://youtu.be/mD8EpWYsP2E
Sombras propias y arrojadas de un sólido
http://youtu.be/G4o2M_BTRYY
Sombra de cuadrado vertical en perspectiva cónica. Luz solar.
http://youtu.be/7zZ3SkIRXls
Sombra de círculo vertical. Cálculo de ejes principales.
http://youtu.be/rT2c-vNMlFY
Penumbra
http://youtu.be/VYUobHA9rjg
Sombra arrojada por un triángulo sobre los 2 planos de proyección del sistema diédrico.
http://youtu.be/e7s1J02opAQ
Sombra distante y puntual de un prisma
http://youtu.be/mD8EpWYsP2E
Sombras propias y arrojadas de un sólido
http://youtu.be/o1WLriEqRg0
Cálculo de sombras y reflexiones en un objeto
http://youtu.be/6HrtuE8BaXU
Sombras propias y arrojadas de otro sólido
http://youtu.be/oMCuvy42EqA
Cálculo de sombras y reflexiones en un objeto
http://youtu.be/6HrtuE8BaXU
Sombras propias y arrojadas de otro sólido
http://youtu.be/oMCuvy42EqA
Sombra propia y arrojada del cono
http://youtu.be/zH0pEMEzN-o
Sombra de cono oblicuo en diédrico
http://youtu.be/qhW0I39QcAI
Sombra de luz puntual de cono apoyado en generatriz. Diédrico.
http://youtu.be/v4XECYgpRqg
Sombra de pirámide sobre plano vertical
http://youtu.be/OsmCF23TDRU
Sombra de cono oblicuo en diédrico
http://youtu.be/qhW0I39QcAI
Sombra de luz puntual de cono apoyado en generatriz. Diédrico.
http://youtu.be/v4XECYgpRqg
Sombra de pirámide sobre plano vertical
http://youtu.be/OsmCF23TDRU
Sombra propia y arrojada de una esfera en sistema diédrico por luz solar
http://youtu.be/CzVvTVHKE3QCálculo de ejes elípticos en sombras de la esfera
http://youtu.be/oJomY7OVJ8I
Sombra de una esfera con luz puntual en sistema diédrico.
http://youtu.be/2qjW8pntCpE
Sombra propia y arrojada del cubo en cónica frontal. Acimut-altitud.
http://youtu.be/Xl1lR_8Y5Sw
Perspectiva cónica frontal y oblicua de 2 cubos y sus sombras
http://youtu.be/Nau68VqUUqI
Sombras del cilindro. Luz puntual y distante.Sistema diédrico.
http://youtu.be/hsQOMibZ6bQ
Sombra de un cilindro oblicuo
http://youtu.be/pnvMwRpVNHY
Sombra autoarrojada de medio cilindro
http://youtu.be/NDBxJt8w4_U
Sombra propia de nicho esférico.Sistema diédrico.
http://youtu.be/3hK8R_b9J20
Sombra de semiesfera hueca.
http://youtu.be/ZB8HEZDfhVY
Sombras propias y arrojadas de un cono invertido.
http://youtu.be/fWP8eeedf38
Sombra de elipsoide en sistema diédrico.
http://youtu.be/4iF5AvhPI9Y
Sombra de pirámide oblicua sobre el plano horizontal y vertical.
http://youtu.be/MtvNFJ5b-eA
Sombras autoarrojadas en el interior de una caja
http://youtu.be/E6GOEgKoTf4
Sombra del toro
http://youtu.be/o4xoFrMkIiw
Cálculo de sombras en una casa en axonometría.
http://youtu.be/00l4wQW7nuI
Cálculo de sombras en una casa en axonometría (con portal y banco).
http://youtu.be/rJqBrq3iQfk
Sombras de objeto con cilindro en cónica
http://youtu.be/5cZaOMkhu5c
Sombras con luz puntual de una pieza
http://youtu.be/WQIpiBUJViA
Sombras de arquitectura con torre y tejado
http://youtu.be/WtEklNDCITI
Sombras sobre una escalera
http://youtu.be/qTy-WRWB04Y
Sombras sobre superficies tangentes y secantes
http://youtu.be/tDycMMXWieI
Sombras de superficies tangentes: cono y esfera
http://youtu.be/1KYuflNBA8I
Sombras de cubos superpuestos en axonometría trimétrica
http://youtu.be/8KeCyVKBPYUBóveda de cañón y su sombra auto-arrojada en perspectiva cónica
http://youtu.be/skwGFjPHZF0
LUSTRE
Dado el brillo de una esfera determinar el punto de luz que la ilumina
http://youtu.be/SmmDj8kYOko
REFLEXIONES
La reflexión sigue las leyes de la perspectiva
http://youtu.be/iDg28iopDf8
Antiarquitectura: reflexión de fachadas a 90°
http://youtu.be/tQSEJeVfZM4
Reflexión como simetría central e homotecia inversa
http://youtu.be/z1BAh7tQcmY
Reflexión de un cuadrado sobre la esfera
http://youtu.be/mO3L7upWRzE
Reflejo de una recta en un cilindro
http://youtu.be/JEx8qPkqjQI
Reflejos en una ventana en interior
http://youtu.be/b41TUQN5KyI
Reflejo de 2 espejos en perspectiva cónica
http://youtu.be/qgcJngPbrtU



